Este apartado trata del Círculo de Quintas (o Círculo de Cuartas; ahora voy a explicar el por qué de la ambigüedad de su nombre).
En un principio, veamos de qué se trata esto con un ejemplo gráfico para facilitar su comprensión:

Si partiendo desde cualquier nota recorremos el círculo en el sentido de las agujas del reloj, estamos avanzando por quintas. Es decir, Sol es la quinta de Do, Re es la quinta de Sol, La es la quinta de Re, y así sucesivamente.
Si recorremos el círculo en el sentido contrario a las agujas del reloj, avanzamos por cuartas. Por eso el mismo gráfico puede tomarse como Círculo de Quintas o Círculo de Cuartas.
En ambos casos, si recorremos todo el círculo, pasamos por todos los nombres de nota de nuestro sistema musical, hasta volver a la nota desde la cual comenzamos.
Este círculo puede utilizarse con distintos propósitos, como hacer progresiones armónicas, modulaciones, y demás recursos. En este caso vamos a utilizarlo para determinar las alteraciones de una Escala Mayor sin necesidad de realizar la suma de Tonos y Semitonos.
Lo primero a definir es si la Escala Mayor en cuestión tiene Sostenidos o Bemoles, cosa que podremos averiguar con las siguientes reglas:
1. La Escala Mayor de Do es la única que no posee ninguna alteración (ni sostenidos ni bemoles).
2. Ninguna Escala Mayor tiene sostenidos y bemoles simultáneamente. O tiene sostenidos o tiene bemoles.
3. La única Escala Mayor cuya Tónica no es bemol y aún así lleva algún bemol en la Escala es la Escala Mayor de Fa, que posee únicamente el Sib.
4. Para el resto de las Escalas Mayores, sólo llevan bemoles aquellas cuya tónica es bemol. Todas las demás, llevan sostenidos.
Averiguar los sostenidos de una Escala Mayor
Para averiguar los sostenidos de una Escala Mayor, vamos a tomar las notas del Círculo de Quintas (en el sentido de las agujas del reloj), comenzando desde Fa.
Por lo tanto, las notas resultantes (y que deben estar grabadas en su cabeza en este orden) son: Fa Do Sol Re La Mi Si.
Repitan estas notas en voz alta en este orden hasta que puedan decirlas sin repetir y sin soplar. Ahora vamos a ver cómo podemos utilizar esto para determinar los sostenidos en una Escala Mayor.
Lo primero a tener en cuenta es que el orden del círculo de quintas es el mismo orden en el que aparecen los sostenidos. Es decir que ninguna Escala Mayor tendrá una de estas notas sostenida sin tener todas las anteriores. Por ejemplo, toda Escala Mayor que tenga el La# también va a tener el Fa#, Do#, Sol# y Re#. Toda aquella que tenga el Sol# también tendrá el Fa# y el Do#.
Ahora vamos a la práctica, con la fórmula para determinar los sostenidos de una Escala Mayor:
1. Restar un semitono a la tónica de la Escala. La nota resultante va a ser el último sostenido de la Escala.
2. Recorrer el Círculo de Quintas hasta llegar a esa nota. Todas las notas recorridas tendrán sostenidos en esta Escala.
Veamos un ejemplo en la Escala de Mi Mayor. Primero escribimos las siete notas sin colocarle alteración a ninguna, comenzando desde la Tónica (es decir, Mi):
E F G A B C D
Ahora aplicamos la fórmula:
Restamos un semitono a Mi y nos da Re#. Esto quiere decir que Re# será el último sostenido de la escala.
Recorremos el círculo de quintas hasta llegar al Re. Las notas resultantes son Fa, Do, Sol y Re. Esas son las notas que tienen sostenidos en la Escala de Mi Mayor. Agregamos un # al lado de cada una de estas notas en la Escala que escribimos antes y el resultado es:
E F# G# A B C# D#
Averiguar los bemoles de una Escala Mayor
En este caso vamos a utilizar las mismas notas del Círculo que antes, pero en el sentido contrario a las agujas del reloj. Es decir que vamos a utilizar el Círculo de Cuartas. Entonces las notas resultantes serían: Si Mi La Re Sol Do Fa.
Repitan las notas en voz alta en ese orden hasta que puedan memorizarlas. Al igual que en el método anterior, el orden del círculo de cuartas es el mismo orden en el que aparecen los bemoles en toda Escala Mayor.
Fórmula para determinar los bemoles de una Escala Mayor:
1. Recorrer el Círculo de Cuartas hasta llegar a la Tónica de la Escala y luego avanzar a la siguiente nota en el Círculo.
2. La nota resultante va a ser el último bemol de la Escala. Todas las notas recorridas tendrán bemoles en esta Escala.
Vamos a ver un ejemplo en Reb. Una vez más, escribimos las notas de la escala sin poner ninguna alteración (en este caso sí le ponemos el bemol al Re, ya que, al ser la tónica, estamos seguros de que lleva un bemol):
Db E F G A B C
Ahora recorremos el círculo de cuartas hasta llegar a la nota siguiente a Re en el círculo. La nota que le sigue a Re en el círculo de cuartas es Sol. Por lo tanto, los bemoles de la escala van a ser Sib, Mib, Lab, Reb y Solb. Los agregamos a las notas que escribimos antes:
Db Eb F Gb Ab Bb C
Alteraciones en Escala Menor
Como vimos anteriormente, toda Escala Menor tiene su Escala Relativa Mayor; es decir, una Escala Mayor que tiene las mismas notas que esta Escala Menor, pero en distinto orden.
Como ya fue explicado, las Escalas Relativas Menores y Mayores se encuentran a una Tercera Menor (1 ½ T) de distancia.
Para determinar los sostenidos o bemoles de una Escala Menor, aplicamos la misma fórmula a su Escala Relativa Mayor.
Por ejemplo, si queremos saber los sostenidos de la escala de Fa# menor, primero buscamos su relativa mayor (La). Ahora escribimos las notas partiendo desde Fa# sin colocar ninguna alteración, excepto en la tónica que ya sabemos que va alterada:
F# G A B C D E
Luego aplicamos la fórmula, pero como si la tónica fuera La. Entonces utilizamos el método para averiguar los sostenidos de la escala de La Mayor. Las notas sostenidas resultantes son F#, C# y G#. Los agregamos a lo escrito antes:
F# G# A B C# D E
Si queremos saber los bemoles de la escala de Sol menor, buscamos su relativa mayor y realizamos el mismo procedimiento. Escribimos las notas sin colocar las alteraciones:
G A B C D E F
Ubicamos la relativa mayor a una tercera menor ascendente, llegando a Sib (no La#, ya que esta no sería la tercera menor sino la segunda aumentada). La escala de Sib tiene bemoles. Utilizamos el método para obtener los bemoles de la escala de Sib.
Las notas resultantes son Bb y Eb. Los agregamos a lo escrito antes:
G A Bb C D Eb F
Escalas con Tónica Alterada
Las Escalas con Tónica Alterada son aquellas cuya tónica ya lleva una alteración.
Cuando hay que elegir entre usar la tónica bemol y la tónica sostenida (por ejemplo, determinar si vamos a utilizar como tónica Do Sostenido o Re bemol), la prioridad es usar la Escala que menos alteraciones tenga (ya sean bemoles o sostenidos).
En lugar de probar las dos opciones y ver cuál de ellas contiene menos alteraciones, existen unas reglas simples, para poder determinarlo rápidamente:
1. Toda Escala Mayor con Tónica Alterada lleva Bemoles.
2. Toda Escala Menor con Tónica Alterada lleva Sostenidos, excepto las dos siguientes:
Sib Menor y Mib Menor (Una forma fácil de recordarlo es que son las 2 primeras notas del Círculo de Cuartas).
Al escribir las alteraciones de una Escala al comienzo de una partitura para indicar la tonalidad en la que se encuentra la obra escrita, dichas alteraciones se escriben con un orden específico de izquierda a derecha: Si son Sostenidos se escriben en el orden del Círculo de Quintas y si son Bemoles se escriben en el orden del Círculo de Cuartas.

Quizás la primera impresión es que este método para determinar las alteraciones de una escala es muy rebuscado, pero les puedo asegurar que, una vez incorporado, es muchísimo más simple, rápido y efectivo que estar contando Tonos y Semitonos.
Bueno, espero que les sirva, cualquier duda consulten.
Saludos.
En un principio, veamos de qué se trata esto con un ejemplo gráfico para facilitar su comprensión:
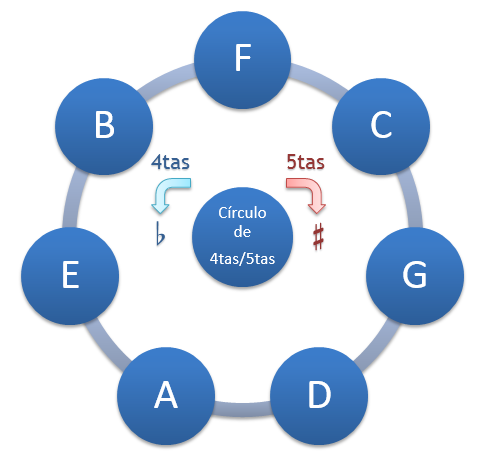
Si partiendo desde cualquier nota recorremos el círculo en el sentido de las agujas del reloj, estamos avanzando por quintas. Es decir, Sol es la quinta de Do, Re es la quinta de Sol, La es la quinta de Re, y así sucesivamente.
Si recorremos el círculo en el sentido contrario a las agujas del reloj, avanzamos por cuartas. Por eso el mismo gráfico puede tomarse como Círculo de Quintas o Círculo de Cuartas.
En ambos casos, si recorremos todo el círculo, pasamos por todos los nombres de nota de nuestro sistema musical, hasta volver a la nota desde la cual comenzamos.
Este círculo puede utilizarse con distintos propósitos, como hacer progresiones armónicas, modulaciones, y demás recursos. En este caso vamos a utilizarlo para determinar las alteraciones de una Escala Mayor sin necesidad de realizar la suma de Tonos y Semitonos.
Lo primero a definir es si la Escala Mayor en cuestión tiene Sostenidos o Bemoles, cosa que podremos averiguar con las siguientes reglas:
1. La Escala Mayor de Do es la única que no posee ninguna alteración (ni sostenidos ni bemoles).
2. Ninguna Escala Mayor tiene sostenidos y bemoles simultáneamente. O tiene sostenidos o tiene bemoles.
3. La única Escala Mayor cuya Tónica no es bemol y aún así lleva algún bemol en la Escala es la Escala Mayor de Fa, que posee únicamente el Sib.
4. Para el resto de las Escalas Mayores, sólo llevan bemoles aquellas cuya tónica es bemol. Todas las demás, llevan sostenidos.
Averiguar los sostenidos de una Escala Mayor
Para averiguar los sostenidos de una Escala Mayor, vamos a tomar las notas del Círculo de Quintas (en el sentido de las agujas del reloj), comenzando desde Fa.
Por lo tanto, las notas resultantes (y que deben estar grabadas en su cabeza en este orden) son: Fa Do Sol Re La Mi Si.
Repitan estas notas en voz alta en este orden hasta que puedan decirlas sin repetir y sin soplar. Ahora vamos a ver cómo podemos utilizar esto para determinar los sostenidos en una Escala Mayor.
Lo primero a tener en cuenta es que el orden del círculo de quintas es el mismo orden en el que aparecen los sostenidos. Es decir que ninguna Escala Mayor tendrá una de estas notas sostenida sin tener todas las anteriores. Por ejemplo, toda Escala Mayor que tenga el La# también va a tener el Fa#, Do#, Sol# y Re#. Toda aquella que tenga el Sol# también tendrá el Fa# y el Do#.
Ahora vamos a la práctica, con la fórmula para determinar los sostenidos de una Escala Mayor:
1. Restar un semitono a la tónica de la Escala. La nota resultante va a ser el último sostenido de la Escala.
2. Recorrer el Círculo de Quintas hasta llegar a esa nota. Todas las notas recorridas tendrán sostenidos en esta Escala.
Veamos un ejemplo en la Escala de Mi Mayor. Primero escribimos las siete notas sin colocarle alteración a ninguna, comenzando desde la Tónica (es decir, Mi):
E F G A B C D
Ahora aplicamos la fórmula:
Restamos un semitono a Mi y nos da Re#. Esto quiere decir que Re# será el último sostenido de la escala.
Recorremos el círculo de quintas hasta llegar al Re. Las notas resultantes son Fa, Do, Sol y Re. Esas son las notas que tienen sostenidos en la Escala de Mi Mayor. Agregamos un # al lado de cada una de estas notas en la Escala que escribimos antes y el resultado es:
E F# G# A B C# D#
Averiguar los bemoles de una Escala Mayor
En este caso vamos a utilizar las mismas notas del Círculo que antes, pero en el sentido contrario a las agujas del reloj. Es decir que vamos a utilizar el Círculo de Cuartas. Entonces las notas resultantes serían: Si Mi La Re Sol Do Fa.
Repitan las notas en voz alta en ese orden hasta que puedan memorizarlas. Al igual que en el método anterior, el orden del círculo de cuartas es el mismo orden en el que aparecen los bemoles en toda Escala Mayor.
Fórmula para determinar los bemoles de una Escala Mayor:
1. Recorrer el Círculo de Cuartas hasta llegar a la Tónica de la Escala y luego avanzar a la siguiente nota en el Círculo.
2. La nota resultante va a ser el último bemol de la Escala. Todas las notas recorridas tendrán bemoles en esta Escala.
Vamos a ver un ejemplo en Reb. Una vez más, escribimos las notas de la escala sin poner ninguna alteración (en este caso sí le ponemos el bemol al Re, ya que, al ser la tónica, estamos seguros de que lleva un bemol):
Db E F G A B C
Ahora recorremos el círculo de cuartas hasta llegar a la nota siguiente a Re en el círculo. La nota que le sigue a Re en el círculo de cuartas es Sol. Por lo tanto, los bemoles de la escala van a ser Sib, Mib, Lab, Reb y Solb. Los agregamos a las notas que escribimos antes:
Db Eb F Gb Ab Bb C
Alteraciones en Escala Menor
Como vimos anteriormente, toda Escala Menor tiene su Escala Relativa Mayor; es decir, una Escala Mayor que tiene las mismas notas que esta Escala Menor, pero en distinto orden.
Como ya fue explicado, las Escalas Relativas Menores y Mayores se encuentran a una Tercera Menor (1 ½ T) de distancia.
Para determinar los sostenidos o bemoles de una Escala Menor, aplicamos la misma fórmula a su Escala Relativa Mayor.
Por ejemplo, si queremos saber los sostenidos de la escala de Fa# menor, primero buscamos su relativa mayor (La). Ahora escribimos las notas partiendo desde Fa# sin colocar ninguna alteración, excepto en la tónica que ya sabemos que va alterada:
F# G A B C D E
Luego aplicamos la fórmula, pero como si la tónica fuera La. Entonces utilizamos el método para averiguar los sostenidos de la escala de La Mayor. Las notas sostenidas resultantes son F#, C# y G#. Los agregamos a lo escrito antes:
F# G# A B C# D E
Si queremos saber los bemoles de la escala de Sol menor, buscamos su relativa mayor y realizamos el mismo procedimiento. Escribimos las notas sin colocar las alteraciones:
G A B C D E F
Ubicamos la relativa mayor a una tercera menor ascendente, llegando a Sib (no La#, ya que esta no sería la tercera menor sino la segunda aumentada). La escala de Sib tiene bemoles. Utilizamos el método para obtener los bemoles de la escala de Sib.
Las notas resultantes son Bb y Eb. Los agregamos a lo escrito antes:
G A Bb C D Eb F
Escalas con Tónica Alterada
Las Escalas con Tónica Alterada son aquellas cuya tónica ya lleva una alteración.
Cuando hay que elegir entre usar la tónica bemol y la tónica sostenida (por ejemplo, determinar si vamos a utilizar como tónica Do Sostenido o Re bemol), la prioridad es usar la Escala que menos alteraciones tenga (ya sean bemoles o sostenidos).
En lugar de probar las dos opciones y ver cuál de ellas contiene menos alteraciones, existen unas reglas simples, para poder determinarlo rápidamente:
1. Toda Escala Mayor con Tónica Alterada lleva Bemoles.
2. Toda Escala Menor con Tónica Alterada lleva Sostenidos, excepto las dos siguientes:
Sib Menor y Mib Menor (Una forma fácil de recordarlo es que son las 2 primeras notas del Círculo de Cuartas).
Al escribir las alteraciones de una Escala al comienzo de una partitura para indicar la tonalidad en la que se encuentra la obra escrita, dichas alteraciones se escriben con un orden específico de izquierda a derecha: Si son Sostenidos se escriben en el orden del Círculo de Quintas y si son Bemoles se escriben en el orden del Círculo de Cuartas.
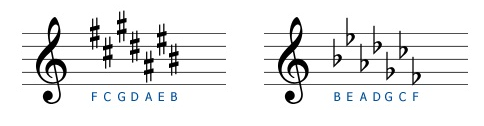
Quizás la primera impresión es que este método para determinar las alteraciones de una escala es muy rebuscado, pero les puedo asegurar que, una vez incorporado, es muchísimo más simple, rápido y efectivo que estar contando Tonos y Semitonos.
Bueno, espero que les sirva, cualquier duda consulten.
Saludos.









