KuRi escribió:
Si, eso que pones es correcto, pero repito, los trastes ya estaban nivelados, por lo que la cantidad a quitar ahora y la cantidad que quedara entre traste y diapason es la misma.
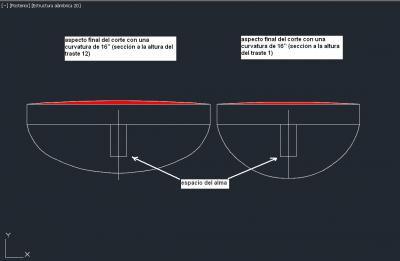
El ejemplo que ha puesto Jors es correctísimo... Pero debes tener en cuenta dos cosas: En primer lugar, que Jors ha dibujado las dos secantes exagerando la longitud de circunferencia que secarían, para que se aprecie claramente la diferencia de altura de los dos segmentos circulares que delimitan, cuando en la realidad, la diferencia de altura de ambos segmentos serían unos 0.6mm. En segundo lugar, que el radio de curvatura no va en los trastes sino en el diapasón, y los trastes simplemente siguen la curvatura del diapasón. Si el radiado del diapasón y el hilo de traste fueran perfectos, y los trastes estuvieran cortados e insertados con un 100% de precisión, no haría falta nivelar los trastes después de trastear. Para cambiar un diapasón de 12" y dejarlo plano, no habría que actuar sobre los trastes, sino directamente sobre el diapasón; y tendríamos que rebajar tanta más altura de madera cuanto más ancho se vaya haciendo el mástil.
KuRi escribió:
Si se usaran tal cual los has puesto en tu dibujo, el trasteo seria total porque el ultimo traste seria mucho mas alto.
En absoluto, porque tanto la cejuela como las selletas del puente continúan el mismo radio; y por lo tanto el puente sería aún más alto que el último traste.
KuRi escribió:
No digo que no tengas razón, pero por matemáticas básicas, si la altura de los trastes es la misma, o al menos están nivelados para que la parte más alta sea la misma, si rebajo más en el último que en el primero, ya no estarán nivelados, irán hacia abajo poco a poco, separándose cada vez más de las cuerdas.
Error. También habría que ajustar el radio y la altura en la selleta y el puente, así que ya no pasaría lo que comentas. Eso no son matemáticas básicas sino percepción espacial errónea. Matemáticas básicas son lo que yo he usado para calcular lo que habría que rebajar en el primer traste y en el último para dejar el radio plano, y es tan simple como calcular el cateto mayor en dos triángulos rectángulos, en los que la hipotenusa (la misma en ambos) son 12" (304.8mm), y los catetos menores son, en el primero la mitad de la anchura del diapasón en la nuez, y en el segundo la mitad de la anchura del diapasón en el zoque.