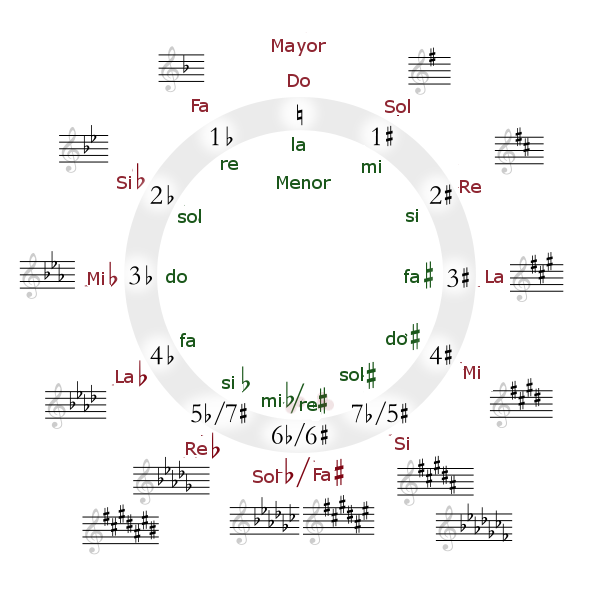
Los Pitagóricos producían los sonidos haciendo vibrar una cuerda y, variando la longitud de esta, obtenían sonidos de distintas alturas, es decir más graves o más agudos. La observación fundamental que hicieron es que dos sonidos tocados simultáneamente resultaban agradables (consonantes) cuando el cociente entre las longitudes de las cuerdas era una fracción cuyo numerador y denominador eran números enteros y pequeños, por ejemplo una el doble de la otra o una el triple de la otra (suponiendo, claro está, que las cuerdas fueran siempre del mismo material y grosor y que estuvieran igualmente tensas).
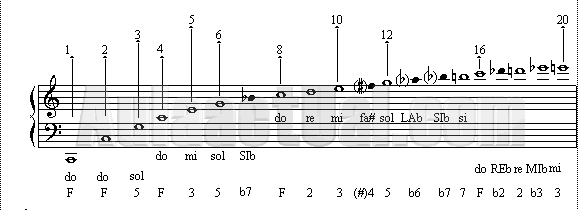
Si por ejemplo partimos de Do
Una cuerda a la mitad da su 8va- Do agudo
Una cuerda en 2/3 da su 5ta - Sol
Una cuerda 3/4 da su 4ta- Fa
La distancia entre Sol y Do es una 4ta
La distancia entre Do y Fa es una 4ta
La distancia entre Do y Sol es una 5ta
La distancia entre Fa y Do es una 5ta
Podemos dividir la 8va en dos partes (dos tetracordios)
Do-re-mi-fa y Sol-la-si-do
En ambos casos estamos a intervalos de 4ta entre sus extremos Do-Fa y Sol-Do. En ambos casos los dos tetracordios son iguales y si lo medimos entre tonos tenemos 2 tonos y medio para llegar a una 4ta.
Pero sucede algo, al buscar (4tas) se puede decir Do-Fa, Re-Sol, Mi-La,Sol-Do, La-Re pero cuando llegamos a Fa-Si eso (No son 2 tonos y medio), tenemos en eso 3 tonos. Estamos hablando de una 4ta aumentada (TRITONO).
Ordenemos los sonidos por 5tas
Do-Sol-Re-La-Mi-Si-Fa#-Do#-Sol#-Re#-La#-(Mi#=Fa)-(Si#=Do)Este último seria la octava.
Tenemos todos los 12 sonidos de la escala ordenados por 5tas, pero Si ordeno las notas en una escala
Do-Re-Mi-Fa-Sol-La-Si-Do Es inevitable encontrarnos con el (TRITONO) entre Fa y Si. Por eso quedan los semitonos y esa medida de semitono es la que se utiliza como patrón para establecer a los 12 sonidos cromáticos, (la escala con sus alteraciones entre #sostenidos y bBemoles).
En el Sistema Pitagórico existía lo que llaman la (coma pitagórica) en donde al llegar a la octava no quedaba perfecta con la primera y se consideraba un 13 décimo tercer sonido que no era exactamente igual a la octava. Con el temperamento igual ya en el barroco se estableció una medida más exacta para poder fijar en un teclado un orden de notas que permita transportar la música a las 12 tonalidades, aunque esa afinación sea modificada levemente para que los sonidos queden equidistantes y no sea una afinación "Natural".
Igualmente esta afinación artificial que puede traernos problemas para afinar pianos y guitarras es la que establece la medida del semitono entre todos los sonidos cromáticos
Do-(Do#=Reb)-Re-(Re#=Mib)-Mi-Fa-(Fa#=Solb)-Sol-(Sol#=Lab)-La-(La#=Sib)-Si-Do
Algunas cuestiones científicas e Históricas entre la afinación pitagórica y el temperamento igual
La existencia de dos semitonos distintos trae consecuencias indeseadas al transportar un motivo musical en un instrumento de afinación fija como el piano. Por ejemplo, si a una melodía que comienza en la nota DO se la transporta subiendo todas sus notas un semitono (es decir comenzándola en DO#) sonará distinta a la original si se usa la escala pitagórica. Esto motivó la construcción de una escala alternativa conocida con el nombre de temperada y que fue comenzada a usar por Johann Sebastián Bach (1685-1750). La idea para construir esta escala es simple: seguir usando doce notas pero cuyas frecuencias sean tales que el cociente entre dos sucesivas resulte siempre igual, es decir, que los semitonos sean todos iguales. La escala así construida resulta muy parecida a la pitagórica
Fuente:
http://mate.dm.uba.ar/~rduran/slides/escalas.pdf
Diferencia entre escala Pitagórica y temperada en Audio, primero Pitagórica, luego Temperada y luego superpuestas
http://mate.dm.uba.ar/~rduran/qed/pitavstemp.wav