Los intervalos se utilizan para expresar las distancias entre las notas de una manera más fácil y práctica que estar contando matemáticamente los Tonos y Semitonos que hay entre ellas. Por ejemplo, si yo me refiero a una nota como "la sexta de Fa", significa que me refiero a la sexta nota contando desde Fa inclusive, es decir contando a Fa como primera. En este caso la nota resultante sería Re (1º Fa, 2º Sol, 3º La, 4º Si, 5º Do, 6º Re).
Ahora, ¿Cómo sé si me refiero a Re, Re# o Reb? Para responder esta pregunta, voy a explicar la clasificación de los intervalos.
Existen dos tipos de intervalos:
Intervalos Perfectos: cuartas, quintas y octavas. Estos intervalos suenan más "huecos" o "carentes de identidad" al ser tocados simultáneamente con la nota en cuestión. Por ejemplo, pueden probar tocar Do y su cuarta (Fa), quinta (Sol) u octava (Do) simultáneamente (sólo una de ellas, es decir primero Do + Fa, después Do + Sol y por último Do + Do). Auditivamente, más que un "agregado", se escucha como un refuerzo de la misma nota.
Intervalos Imperfectos: segundas, terceras, sextas y séptimas. Estos intervalos tienen más identidad propia, y, de tocarse simultáneamente con la nota en cuestión, es más fácil al oído escuchar que están sonando dos notas al mismo tiempo.
A su vez, cada tipo de intervalo tiene diversas clasificaciones:
Un Intervalo Perfecto puede ser: Justo, Aumentado o Disminuido. Para aclarar esto, vamos a poner un ejemplo:
Sol es la Quinta Justa de Do. Si yo le agrego un # a ese Sol, estoy aumentando la distancia entre ambas notas. Al aumentar un Intervalo Justo, lo convierto en Aumentado (valga la redundancia). Es decir que Sol# es la Quinta Aumentada de Do. Si por el contrario le agrego un bemol al Sol, acortaría la distancia desde Do. Al disminuir un Intervalo Justo, lo convierto en Disminuido (valga una vez más la redundancia). Entonces Solb es la Quinta disminuida de Do.
Un Intervalo Imperfecto puede ser, en un principio, Mayor o Menor. Por ejemplo, La es la Sexta Mayor de Do. Si le agrego un bemol al La, convirtiéndola en un Lab, acorto la distancia entre ambas notas. Al disminuir un Intervalo Mayor lo convierto en Menor. Por lo tanto, Lab es la Sexta Menor de Do.
Para el caso contrario pongamos como ejemplo a Sol, que es la Tercera Menor de Mi. Si le agrego un # al Sol, convirtiéndolo en un Sol#, aumento la distancia entre ambas notas. Al aumentar un Intervalo Menor lo convierto en Mayor. Por lo tanto, Sol# es la Tercera Mayor de Mi.
Y, ¿Qué pasa si aumento un Intervalo Mayor o disminuyo un Intervalo Menor? Lo convierto en Aumentado o Disminuido respectivamente.
Por ejemplo, Re es la Segunda Mayor de Do. Si lo transformo en Re#, teniendo en cuenta que al aumentar un Intervalo Mayor lo convierto en Aumentado, obtengo como resultado la Segunda Aumentada de Do. Para el caso contrario, tomemos el caso de Sol como Séptima Menor de La. Si lo transformo en un Solb, teniendo en cuenta que al disminuir un Intervalo Menor lo convierto en Disminuido, obtengo como resultado la Séptima Disminuida de La.
Seguramente, espero, se estarán preguntando ¿Y cómo se cuál es la Cuarta Aumentada de La, o cualquier otro intervalo?
Hay dos maneras: una es sabiendo de memoria todos los intervalos y su equivalente en Tonos y Semitonos. Este método es engorroso y poco efectivo en un principio. Con el tiempo uno los va memorizando de calcularlos tantas veces, pero no recomiendo intentar tenerlos de memoria en un principio.
El otro método es tomando como referencia la Escala Mayor. Para esto es necesario saber que en cualquier Escala Mayor, contando la distancia desde la Tónica hasta cualquier nota de la escala, todos los Intervalos Perfectos son Justos y todos los Intervalos Imperfectos son Mayores.
Para aclarar, dejo un gráfico de la Escala Mayor de Do, especificando los intervalos entre Do (la Tónica de la escala) y cada una de las otras notas de la escala.

Como ven, todos los intervalos son Justos y Mayores, tal y como dije antes. Entonces, para saber cuál es la distancia equivalente a una Cuarta Justa, hay que contar la distancia entre la Tónica y la Cuarta en una Escala Mayor. En este caso, escala de Do, contaríamos la distancia entre Do y Fa, que nos daría 2 tonos y medio. Luego, si quieren saber la distancia equivalente a un intervalo
menor, disminuido o aumentado, sólo queda sumar o restar un semitono a la distancia deseada. Es importante tener en cuenta que siempre que se habla de aumentar o disminuir, es en términos de un semitono. Para la Sexta y la Séptima recomiendo contar su distancia hasta la Octava, ya que es mucho menor que desde la Tónica. Por ejemplo, la Sexta Mayor está a un tono y medio de la octava, y la Séptima Mayor a un semitono.
Teniendo en claro las categorías y los diversos valores posibles de intervalos, pueden, en un principio, entender la diferencia entre dos notas enarmónicas. Por notas enarmónicas nos referimos a dos notas que suenan igual pero se llaman distinto, por ejemplo Sol# y Lab. Para explicar cómo influyen los intervalos a distinguir las enarmonías, voy a poner el siguiente ejemplo:
Si yo quiero armar una escala de Do que sea igual a la Escala Mayor pero con la Sexta Menor, obtendría las siguientes notas:
Do - Re - Mi - Fa - Sol - Lab - Si.
En cambio, si quisiera una escala igual a la Escala Mayor de Do pero con la Quinta Aumentada, sus notas serían:
Do - Re - Mi - Fa - Sol# - La - Si.
Siempre que tengamos una escala de siete notas tenemos que nombrar a todas las siete notas distintas y no repetir ninguna de ellas al alterarla. Por ejemplo, decir que las últimas tres notas de la primera escala mencionada son Sol, Sol# y Si sería incorrecto, ya que estoy repitiendo el Sol y estoy omitiendo el La. De la misma manera y por el mismo motivo sería incorrecto decir que son Lab, La y Si. De esta manera es más fácil observar la diferencia entre las dos escalas que puse como ejemplo: en la primera se modifica el Sol (la Quinta) y el La queda igual, mientras que en la segunda se modifica el La (la Sexta) y el Sol queda igual.
A continuación les dejo una Tabla de Intervalos y su respectivo equivalente en Tonos y Semitonos. Esta tabla no es con el objetivo de que la memoricen, sino para tener como referencia de consulta.

Resumen
Hay dos tipos de intervalos: los Perfectos (cuarta, quinta y octava) y los Imperfectos (segunda, tercera, sexta y séptima).
Los Intervalos Perfectos se clasifican de la siguiente manera, de menor a mayor:
-< Disminuido___Justo___Aumentado >+
Los Intervalos Imperfectos se clasifican de la siguiente manera, de menor a mayor:
-< Disminuido___Menor___Mayor___Aumentado >+
En toda Escala Mayor, todos los Intervalos Perfectos son Justos y todos los Intervalos Imperfectos son Mayores.
Consonancias y disonancias
Todos los intervalos que nombramos, en todas sus categorías, pueden ser divididos en dos grupos: consonancias y disonancias. La diferencia entre ambos grupos es auditiva: la disonancia genera tensión y la consonancia genera distensión.
Podríamos enumerar cada intervalo indicando si es consonancia o disonancia, pero vamos a resumir todo con este conjunto de 4 reglas:
1) Todos los Intervalos Justos son Consonancias
2) Todos los Intervalos Aumentados y Disminuidos son Disonancias
3) La Tercera y la Sexta, tanto Mayores como Menores, son Consonancias
4) La Segunda y la Séptima, tanto Mayores como Menores, son Disonancias
Bueno, esto es todo por hoy. Espero que les sirva, cualquier cosa que no se entienda no duden en consultar. Hasta la próxima.
Saludos
Ahora, ¿Cómo sé si me refiero a Re, Re# o Reb? Para responder esta pregunta, voy a explicar la clasificación de los intervalos.
Existen dos tipos de intervalos:
Intervalos Perfectos: cuartas, quintas y octavas. Estos intervalos suenan más "huecos" o "carentes de identidad" al ser tocados simultáneamente con la nota en cuestión. Por ejemplo, pueden probar tocar Do y su cuarta (Fa), quinta (Sol) u octava (Do) simultáneamente (sólo una de ellas, es decir primero Do + Fa, después Do + Sol y por último Do + Do). Auditivamente, más que un "agregado", se escucha como un refuerzo de la misma nota.
Intervalos Imperfectos: segundas, terceras, sextas y séptimas. Estos intervalos tienen más identidad propia, y, de tocarse simultáneamente con la nota en cuestión, es más fácil al oído escuchar que están sonando dos notas al mismo tiempo.
A su vez, cada tipo de intervalo tiene diversas clasificaciones:
Un Intervalo Perfecto puede ser: Justo, Aumentado o Disminuido. Para aclarar esto, vamos a poner un ejemplo:
Sol es la Quinta Justa de Do. Si yo le agrego un # a ese Sol, estoy aumentando la distancia entre ambas notas. Al aumentar un Intervalo Justo, lo convierto en Aumentado (valga la redundancia). Es decir que Sol# es la Quinta Aumentada de Do. Si por el contrario le agrego un bemol al Sol, acortaría la distancia desde Do. Al disminuir un Intervalo Justo, lo convierto en Disminuido (valga una vez más la redundancia). Entonces Solb es la Quinta disminuida de Do.
Un Intervalo Imperfecto puede ser, en un principio, Mayor o Menor. Por ejemplo, La es la Sexta Mayor de Do. Si le agrego un bemol al La, convirtiéndola en un Lab, acorto la distancia entre ambas notas. Al disminuir un Intervalo Mayor lo convierto en Menor. Por lo tanto, Lab es la Sexta Menor de Do.
Para el caso contrario pongamos como ejemplo a Sol, que es la Tercera Menor de Mi. Si le agrego un # al Sol, convirtiéndolo en un Sol#, aumento la distancia entre ambas notas. Al aumentar un Intervalo Menor lo convierto en Mayor. Por lo tanto, Sol# es la Tercera Mayor de Mi.
Y, ¿Qué pasa si aumento un Intervalo Mayor o disminuyo un Intervalo Menor? Lo convierto en Aumentado o Disminuido respectivamente.
Por ejemplo, Re es la Segunda Mayor de Do. Si lo transformo en Re#, teniendo en cuenta que al aumentar un Intervalo Mayor lo convierto en Aumentado, obtengo como resultado la Segunda Aumentada de Do. Para el caso contrario, tomemos el caso de Sol como Séptima Menor de La. Si lo transformo en un Solb, teniendo en cuenta que al disminuir un Intervalo Menor lo convierto en Disminuido, obtengo como resultado la Séptima Disminuida de La.
Seguramente, espero, se estarán preguntando ¿Y cómo se cuál es la Cuarta Aumentada de La, o cualquier otro intervalo?
Hay dos maneras: una es sabiendo de memoria todos los intervalos y su equivalente en Tonos y Semitonos. Este método es engorroso y poco efectivo en un principio. Con el tiempo uno los va memorizando de calcularlos tantas veces, pero no recomiendo intentar tenerlos de memoria en un principio.
El otro método es tomando como referencia la Escala Mayor. Para esto es necesario saber que en cualquier Escala Mayor, contando la distancia desde la Tónica hasta cualquier nota de la escala, todos los Intervalos Perfectos son Justos y todos los Intervalos Imperfectos son Mayores.
Para aclarar, dejo un gráfico de la Escala Mayor de Do, especificando los intervalos entre Do (la Tónica de la escala) y cada una de las otras notas de la escala.
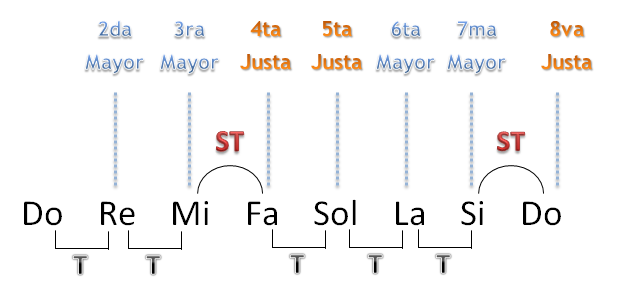
Como ven, todos los intervalos son Justos y Mayores, tal y como dije antes. Entonces, para saber cuál es la distancia equivalente a una Cuarta Justa, hay que contar la distancia entre la Tónica y la Cuarta en una Escala Mayor. En este caso, escala de Do, contaríamos la distancia entre Do y Fa, que nos daría 2 tonos y medio. Luego, si quieren saber la distancia equivalente a un intervalo
menor, disminuido o aumentado, sólo queda sumar o restar un semitono a la distancia deseada. Es importante tener en cuenta que siempre que se habla de aumentar o disminuir, es en términos de un semitono. Para la Sexta y la Séptima recomiendo contar su distancia hasta la Octava, ya que es mucho menor que desde la Tónica. Por ejemplo, la Sexta Mayor está a un tono y medio de la octava, y la Séptima Mayor a un semitono.
Teniendo en claro las categorías y los diversos valores posibles de intervalos, pueden, en un principio, entender la diferencia entre dos notas enarmónicas. Por notas enarmónicas nos referimos a dos notas que suenan igual pero se llaman distinto, por ejemplo Sol# y Lab. Para explicar cómo influyen los intervalos a distinguir las enarmonías, voy a poner el siguiente ejemplo:
Si yo quiero armar una escala de Do que sea igual a la Escala Mayor pero con la Sexta Menor, obtendría las siguientes notas:
Do - Re - Mi - Fa - Sol - Lab - Si.
En cambio, si quisiera una escala igual a la Escala Mayor de Do pero con la Quinta Aumentada, sus notas serían:
Do - Re - Mi - Fa - Sol# - La - Si.
Siempre que tengamos una escala de siete notas tenemos que nombrar a todas las siete notas distintas y no repetir ninguna de ellas al alterarla. Por ejemplo, decir que las últimas tres notas de la primera escala mencionada son Sol, Sol# y Si sería incorrecto, ya que estoy repitiendo el Sol y estoy omitiendo el La. De la misma manera y por el mismo motivo sería incorrecto decir que son Lab, La y Si. De esta manera es más fácil observar la diferencia entre las dos escalas que puse como ejemplo: en la primera se modifica el Sol (la Quinta) y el La queda igual, mientras que en la segunda se modifica el La (la Sexta) y el Sol queda igual.
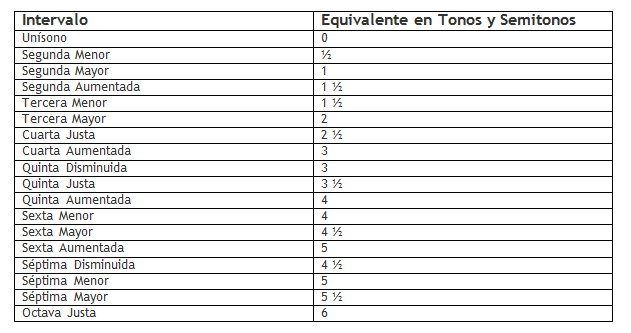
A continuación les dejo una Tabla de Intervalos y su respectivo equivalente en Tonos y Semitonos. Esta tabla no es con el objetivo de que la memoricen, sino para tener como referencia de consulta.
Resumen
Hay dos tipos de intervalos: los Perfectos (cuarta, quinta y octava) y los Imperfectos (segunda, tercera, sexta y séptima).
Los Intervalos Perfectos se clasifican de la siguiente manera, de menor a mayor:
-< Disminuido___Justo___Aumentado >+
Los Intervalos Imperfectos se clasifican de la siguiente manera, de menor a mayor:
-< Disminuido___Menor___Mayor___Aumentado >+
En toda Escala Mayor, todos los Intervalos Perfectos son Justos y todos los Intervalos Imperfectos son Mayores.
Consonancias y disonancias
Todos los intervalos que nombramos, en todas sus categorías, pueden ser divididos en dos grupos: consonancias y disonancias. La diferencia entre ambos grupos es auditiva: la disonancia genera tensión y la consonancia genera distensión.
Podríamos enumerar cada intervalo indicando si es consonancia o disonancia, pero vamos a resumir todo con este conjunto de 4 reglas:
1) Todos los Intervalos Justos son Consonancias
2) Todos los Intervalos Aumentados y Disminuidos son Disonancias
3) La Tercera y la Sexta, tanto Mayores como Menores, son Consonancias
4) La Segunda y la Séptima, tanto Mayores como Menores, son Disonancias
Bueno, esto es todo por hoy. Espero que les sirva, cualquier cosa que no se entienda no duden en consultar. Hasta la próxima.
Saludos









